Free PHPFree PHP scripts classes and info

WebAudio Deep Note, part 1

You've heard of WebAudio, but have you done any experimenting with it? This is a series of posts on exploring and discovering various APIs that WebAudio has to offer, by doing something concrete, namely recreate the THX Deep Note sound.

If you cannot wait for me to write up everything, the code and slides (these posts are based on a talk) are on Github and also here.

Deep Note?

You don't know what Deep Note is? Yes, you do! Here's an example to refresh your memory:

This is a sort of an audio logo that was meant to be used with the THX visual logo. The engineer who coded the audio logo, James Andy Moorer, tells the story in this 2-part podcast. It's actually pretty entertaining. There's some more info thanks to his son, who's on Reddit.

The idea was to create a sound that comes out of nowhere, out of chaos and turns into something meaningful. Chaos to order. Mr.Moore was inspired by two pieces: one by J.S.Bach (start at 0:20) and one by The Beatles (start at 3:30 mark).

The "score"

Oh and the "score" for the composition was released not too long ago:

So what do we know?

After listening to the interviews and reading the comments on Reddit, what do we know about how Mr.Moorer decided to approach creating this signature sound? And what we can do to mimic the process as close as possible?

• There are 30 "voices" (distinct sounds), because this was the limitation of the ASP (Audio Signal Processor) that was available at the time.
• There are 11 notes in the score. So - 11 notes and 30 voices. Which voice plays which note? The score says the top note is played by three voices, and the two bottom ones by 2 voices each. That makes 8 (middle) + 3 (top) + 4 (bottom) = 15. My guess is then every one of these voices was doubled again, so that's 8 x 2 (middle), top note x 6, 2 bottom ones x 4. Total of 30. It's inconceivable to think he had access to 30 voices and didn't use them all!
• Each voices changes pitch over time. They start as a tight cluster (200 to 400Hz), wiggle around a bit and then slowly move to their final destinations of the final chord.
• Each voice plays and manipulates a single cello sample. Most of the notes are D (the final chord is D major) so probably the sample was D too. But because we can re-pitch it (and we have to, see next point) we can start with any old sample. I found one C on the web and thought I should start there. So obviously right off the bat we lose all hope of recreating the exact same end effect, but that's not the ultimate purpose of these posts. We're here to learn WebAudio. Plus the cello sample is actually from a synthesizer, so maybe not a real cello at all. Plus, the program that Mr.Moorer created is random and they actually had troubles recreating the same result with the same program after they lost the original recording. Heee-heee.
• The D (D3, meaning the first D below middle C) was pitched to 150Hz. Which is not what our current Western equal temperament tuning is using. We're used to D3 being 146.83Hz. But 150 is easier to multiply (or reason about), I guess. And maybe this tiny discrepancy (150 is between D3 and the next D#3) just helps make the sound more alien and interesting (wild guess). FYI the nice round number the modern Western equal temperament is using is actually 440Hz, the A above middle C.
• He used just tuning as opposed to equal temperament tuning. It's a fascinating thing, tuning systems. Feel free to skip, but I'll try a short explanation. Ancient Greeks, obsessed with perfection and ratios, figured that when two notes sound good together, the string that produces the first note is double the length of the second. Which is also double the frequency. This is what we call an interval of an octave now. A4 is 440Hz, the next A (A5) is 880Hz. A3 is 220, and so on. So 2:1 ratio. Next 3:2 ratio also sounds good together. And 4:3. These 3 ratios are so perfect that they are still called perfect today: perfect octave, perfect fifth, perfect fourth.
  
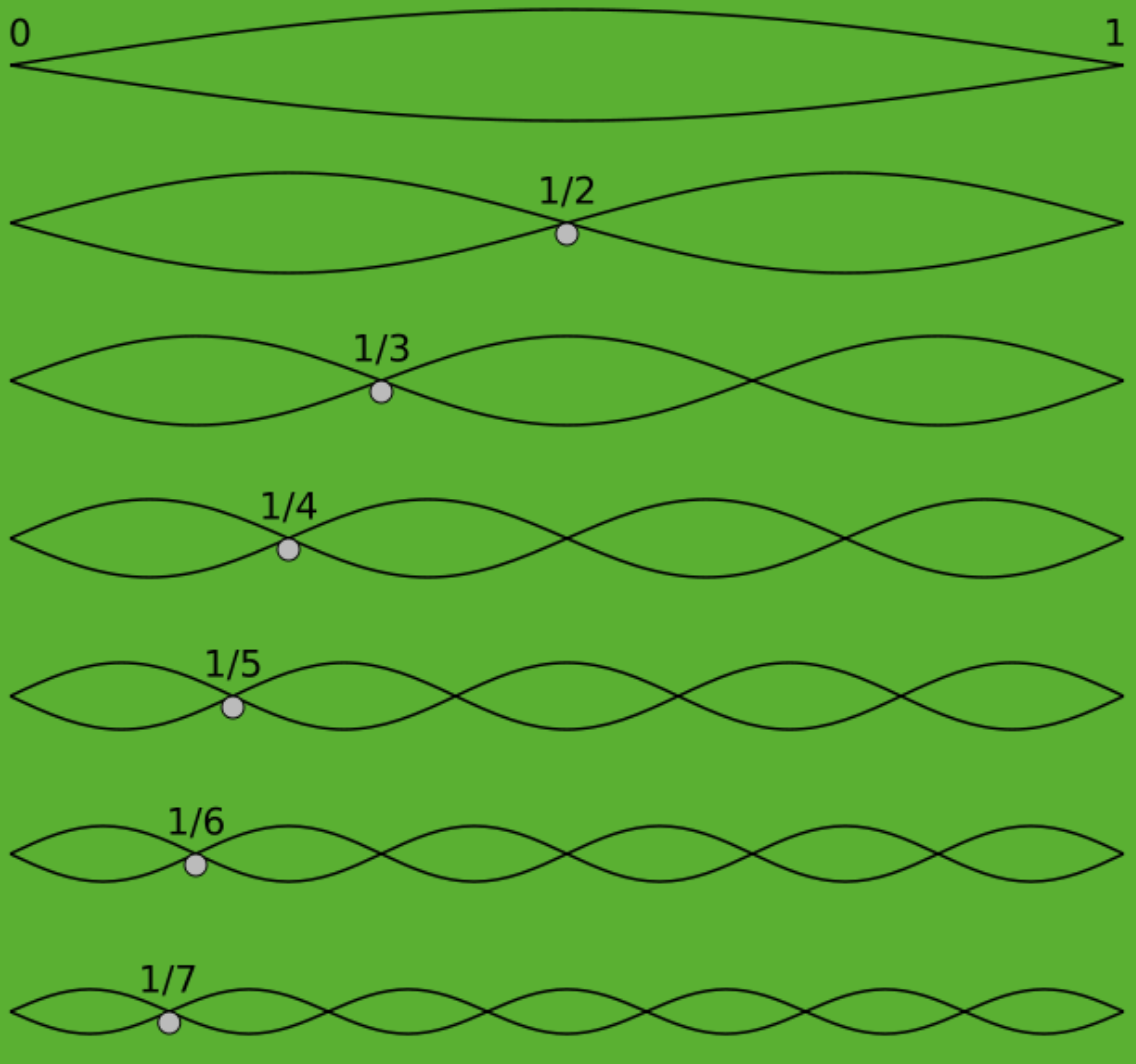
  The problem (called Pythagorean comma) is that if you continue diving the string in perfect ratios, you don't get the same note an octave above. Bummer! For the longest time people dealt with this by slightly compensating some of the notes, to taste. Eventually equal temperament was invented where we said "Enough! Divide the octave into twelve notes with equal ratios between them!" The ratio is 12th root of 2, or about 1.05946. As a result nothing is ever perfectly in tune (except octaves). As opposed so some notes not in tune. But we got used to it. Singing doesn't have fixed pitches, so you can still hear perfectly tuned chords in vocal music, e.g. choirs and barbershop quartets. But for the most part, it's rare for us today to hear. Deep Note's chord though is perfectly tuned, maybe that's another reason for it sounding a tad alien. The chord is a D major which means it has three notes: D, A and F# and they are repeated. A lot of Ds, some As and a single F#. All Ds are 2:1, the As are 3:2 and the F# is 4:3

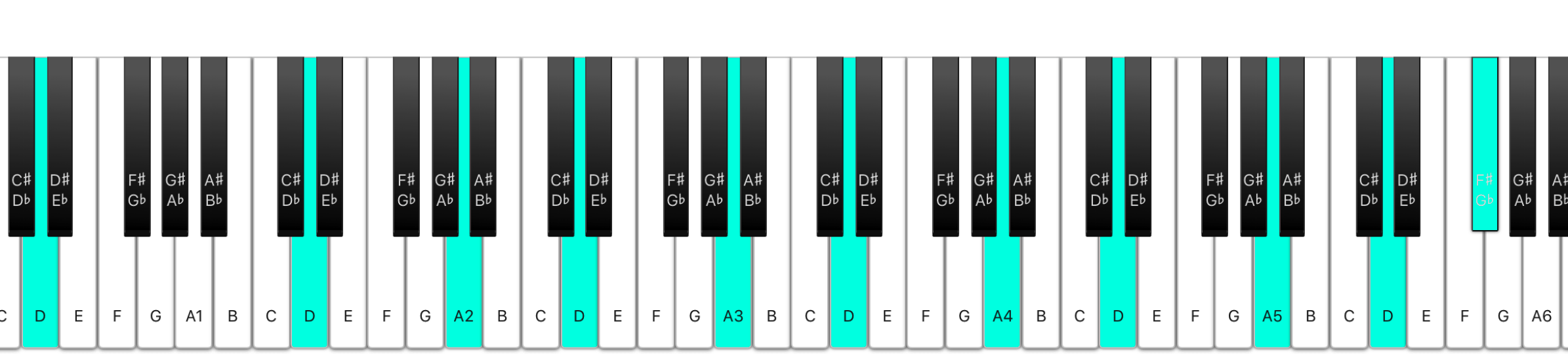
So the notes of our final chord will be:

const notes = {
  D1: {rate: 1/4, voices: 4},
  D2: {rate: 1/2, voices: 4},
  A2: {rate: 3/4, voices: 2},
  D3: {rate: 1,   voices: 2},
  A3: {rate: 3/2, voices: 2},
  D4: {rate: 2,   voices: 2},
  A4: {rate: 3,   voices: 2},
  D5: {rate: 4,   voices: 2},
  A5: {rate: 6,   voices: 2},
  D6: {rate: 8,   voices: 2},
  Fs: {rate: 10,  voices: 6},
};

And this is how the notes look on the piano keyboard (the picture is from my web midi keyboard, check it out):

Alrighty

That's enough verbiage to get us off the ground, let's start making some noise in the next post! The plan of attack is to learn about WebAudio in this manner:

1. Learn to play one sound - our cello sample. Fetch from the server, decode the audio, createBufferSource(), connect it to the speakers/headphones and start it. We'll have to deal with some Safari inconsistencies.
2. Learn about how WebAudio uses nodes that you connect together.
3. Loop the sound using the loop property of the buffer source object. The sample is too short and the deep note is a little longer.
4. Repitch the sound using the playbackRate property of the buffer source. We need to do this because the sample is C not D and also the D is the weird 150Hz and also there are 11 distinct notes. So whole lotta pitching.
5. Play 30 notes using 30 buffers from the same sample. Learn about the Gain (volume) node otherwise 30 simultaneous notes are a little loud.
6. Learn about scheduling changes with setValueAtTime(), linearRampToValueAtTime(), exponentialRampToValueAtTime() and setTargetAtTime(). This is because the voices change frequencies. And volume.
7. Figure out a bunch of sweeteners: compression (even out peaks), EQ (filtering frequencies), reverb (like echo, using convolution), and panning (moving from one speaker to the other).
8. Signal flow: creating a graph of WebAudio nodes, split the signal, apply different processing to different part of it, merge back.
9. Record the results so we can put them on the radio!
10. Visualize what we've done with these frequencies.

Fun times ahead!